Phương pháp giải:

+) Dựng mặt phẳng \(\left( AEF \right)\)sao cho \(\left( AEF \right)\bot SM\).

+) Dựa  vào công thức tỉ lệ thể tích để suy ra vị trí của các điểm \(E,F\).

+) Tính thể tích khối chóp theo công thức \(V=\frac{1}{3}h.S\).

Lời giải chi tiết:

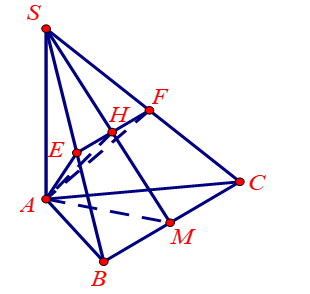
Từ \({{V}_{S.AEF}}=\frac{1}{4}{{V}_{S.ABC}}\Rightarrow \frac{{{V}_{S.AEF}}}{{{V}_{S.ABC}}}=\frac{1}{4}\)\(\Rightarrow \frac{SE}{SB}.\frac{SF}{SC}=\frac{1}{4}\)

Suy ra \(E,F\) là trung điểm của \(SB,SC\)

Kẻ \(AH\bot SM\) \(\Rightarrow H\in EF\)\(\Rightarrow AH=HM\) (Do\(\Delta SAM\) vuông tại)

\(\Rightarrow \Delta AMH\) vuông cân tại \(H\) \(\Rightarrow \widehat{AMH}={{45}^{0}}\)

\(\Rightarrow SA=AM=\frac{a\sqrt{3}}{2}\)

\(\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}.SA.{{S}_{\Delta ABC}}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}}{8}\)

Chọn B.