Phương pháp giải:

+) Xác định chiều cao từ \(M\) xuống mặt phẳng \(\left( {A}'{B}'{C}'{D}' \right)\).

+) Tính thể tích khối chóp theo công thức \(V=\frac{1}{3}h.S\) với \(h\) là chiều cao, \(S\) là diện tích đáy.

Lời giải chi tiết:

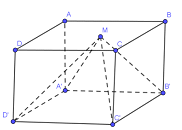
Ta có \(\left( ABCD \right)//\left( {A}'{B}'{C}'{D}' \right)\)và \(M\in \)\(\left( ABCD \right)\) nên khoảng cách từ M đến \(\left( {A}'{B}'{C}'{D}' \right)\) bằng khoảng cách giữa hai mặt phẳng \(\left( ABCD \right)\) và \(\left( {A}'{B}'{C}'{D}' \right)\)và bằng chiều cao \(h\) của khối lăng trụ \(ABCD.{A}'{B}'{C}'{D}'\). Ta có \({{V}_{LT}}={{S}_{{A}'{B}'{C}'{D}'}}.h\) mặt khác \({{V}_{M.{A}'{B}'{C}'{D}'}}\)\(=\frac{1}{3}{{S}_{{A}'{B}'{C}'{D}'}}.h\)\(=\frac{1}{3}{{V}_{LT}}\)\(=\frac{1}{3}.36=12\text{ }c{{m}^{3}}.\)

Chọn A.