Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( ABCD \right)\) trùng với trung điểm của cạnh \(AD\), \(SB\) hợp với đáy một góc \({{60}^{o}}\). Tính theo \(a\) thể tích Vcủa khối chóp \(S.ABCD\)
- A \(V=\frac{{{a}^{3}}\sqrt{15}}{2}\).
- B \(V=\frac{{{a}^{3}}\sqrt{15}}{6}\).
- C \(V=\frac{{{a}^{3}}\sqrt{5}}{4}\).
- D \(V=\frac{{{a}^{3}}\sqrt{5}}{\sqrt{3}}\)
Phương pháp giải:
+) Xác định góc giữa đường thẳng d và mặt phẳng (P): là góc giữa hình chiếu d’ của d xuống (P) với đường thẳng d.
+) Sử dụng công thức tính thể tích khối chóp \(V=\frac{1}{3}h.S\) với \(h\) là chiều cao hình chóp hạ từ đỉnh, \(S\) là diện tích đáy.
Lời giải chi tiết:
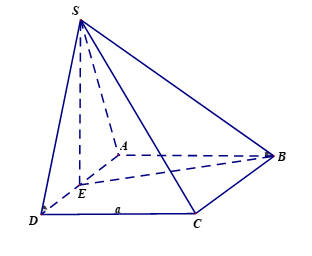
Gọi \(E\) trung điểm của \(AD\). Khi đó \(SE\bot \left( ABCD \right)\).
\(V=\frac{1}{3}{{S}_{ABCD}}.SE\)
\({{S}_{ABCD}}={{a}^{2}}\)
\(EB\) là hình chiếu của \(SB\) lên mặt phẳng \(\left( ABCD \right)\).
\(\Rightarrow \widehat{\left( SB,\left( ABCD \right) \right)}=\widehat{SBE}={{60}^{o}}\)
\(BE=\sqrt{A{{E}^{2}}+A{{B}^{2}}}=\sqrt{\frac{{{a}^{2}}}{4}+{{a}^{2}}}=\frac{a\sqrt{5}}{2}\)
\(SE=\tan {{60}^{o}}.BE=\frac{a\sqrt{15}}{2}\)
Vậy \(V=\frac{1}{3}.\frac{a\sqrt{15}}{2}.{{a}^{2}}=\frac{{{a}^{3}}\sqrt{15}}{6}\).
Chọn B.







