Câu hỏi
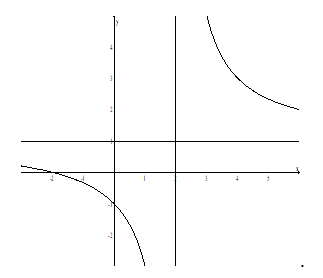
Đường cong ở hình bên là đồ thị hàm số \(y=\frac{ax+2}{cx+b}\) với \(a,b,C\)là các số thực. Mệnh đề nào sau đây đúng ?
- A \(a=2;b=2;c=-1\).
- B \(a=1;b=-2;c=1\).
- C \(a=1;b=2;c=1\).
- D \(a=1;b=1;c=-1\).
Phương pháp giải:
Sử dụng kiến thức về tiệm cận và giao của đồ thị hàm số với các trục tọa độ
Lời giải chi tiết:
Vì đồ thị hàm số nhận đường thẳng \(y=1;x=2\) làm đường tiệm cận ngang và tiệm cận đứng và đồ thị hàm số cắt \(Oy\)tại điểm có tung độ bằng \(-1\)nên ta có hệ :
\(\left\{ {\begin{array}{*{20}{c}}{ - \frac{b}{c} = 2}\\{\frac{a}{c} = 1}\\{\frac{2}{b} = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 2}\\{c = 1}\end{array}} \right.\) .
Chọn B .







