Phương pháp giải:

Sử dụng bất đẳng thức tam giác \(IM+MN\ge IN\Leftrightarrow MN\ge IN-R\Rightarrow MN\,\,\min \Leftrightarrow NI\,\,\min \)

Lời giải chi tiết:

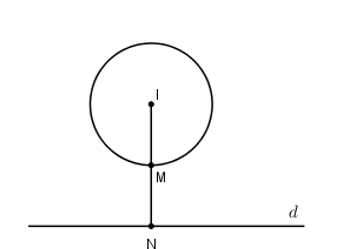
Đường tròn (C ) có tâm \(I(-1;3)\) và bán kính \(R=\sqrt{{{\left( -1 \right)}^{2}}+{{3}^{2}}-9}=2\).

Ta có: \(d(I;d)=\frac{\left| 3.\left( -1 \right)-4.3+5 \right|}{\sqrt{{{3}^{2}}+{{4}^{2}}}}=2>R\)

Suy ra \(d\) không cắt (C ).

Ta có \(IM+MN\ge IN\Leftrightarrow MN\ge IN-R\)  

MN min \(\Leftrightarrow \)  IN đạt min \(\Leftrightarrow \) N là chân hình chiếu vuông góc của I xuống đường thẳng d.

Giả sử \(N(a;b)\). Vì \(N\in d\) nên ta có \(3a\text{ - }4b\text{ }+\text{ }5\text{ }=\text{ }0\) (1)

Mặt khác, ta có: IN vuông góc với d nên \(\overrightarrow{IN}.\overrightarrow{{{u}_{d}}}=0\). Mà \(\overrightarrow{IN}=\left( a+1;b-3 \right),\overrightarrow{{{u}_{d}}}=\left( 4;3 \right)\). Suy ra ta có: \(4(a+1)+3(b-3)=0\Leftrightarrow 4a+3b-5=0\)   (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}4a + 3b - 5 = 0\\3a - 4b + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{5}\\b = \frac{7}{5}\end{array} \right. \Rightarrow N\left( {\frac{1}{5};\frac{7}{5}} \right)\)

Vì \(d(I;d)=2R\) nên \(M\) là trung điểm của \(IN\). Do đó, tọa độ của \(M\) là:

\(\left\{ \begin{array}{l}{x_M} = \frac{1}{2}\left( { - 1 + \frac{1}{5}} \right) =  - \frac{2}{5}\\{y_M} = \frac{1}{2}\left( {3 + \frac{7}{5}} \right) = \frac{{11}}{5}\end{array} \right. \Rightarrow M\left( { - \frac{2}{5};\frac{{11}}{5}} \right)\)

Chọn B.