Câu hỏi
Cho đường tròn \((C):{{x}^{2}}+{{y}^{2}}-4x-2y=0\) và đường thẳng\(d:x-y+1=0\). Tìm mệnh đề đúng trong các mệnh đề sau:
- A \(d\) đi qua tâm của \((C)\).
- B \(d\) cắt \((C)\) tại hai điểm.
- C \(d\) tiếp xúc với \((C)\) .
- D \(d\) không có điểm chung với \((C)\).
Phương pháp giải:
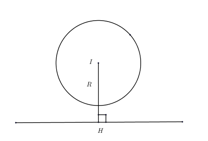
\(\left( C \right)\) tâm \(I\left( a;b \right)\), bán kính \(R\), đường thẳng \(d:A\,x+B\,y+C=0\)
Gọi \(IH=d\left( I,d \right)\)
+) \(IH>R\Leftrightarrow d\) không có điểm chung với \(\left( C \right)\)
+) \(IH=R\Leftrightarrow d\) tiếp xúc với \(\left( C \right)\)
+)\)IH<R\Leftrightarrow d\) cắt \(\left( C \right)\) tại hai điểm phân biệt.
Lời giải chi tiết:
\((C):{{x}^{2}}+{{y}^{2}}-4x-2y=0\) có tâm \(I(2;1)\) và bán kính \(R=\sqrt{{{2}^{2}}+{{1}^{2}}}=\sqrt{5}\)
Ta có \(IH=d\left( I,d \right)=\frac{|2-1+1|}{\sqrt{2}}=\sqrt{2}<R\). Suy ra \(IH<R\Leftrightarrow d\) cắt \(\left( C \right)\) tại hai điểm phân biệt.
Chọn B.







