Phương pháp giải:

- Lập tỉ số thể tích \(\frac{{{V}_{OABH}}}{{{V}_{OABI}}};\,\,\frac{{{V}_{AOBI}}}{{{V}_{OABC}}}\)

- Tính thể tích \({{V}_{OABH}}\)thông qua \({{V}_{OABC}}\). 

Lời giải chi tiết:

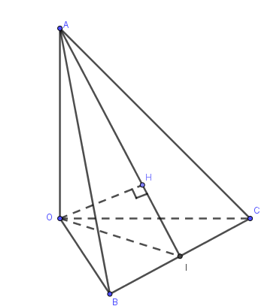
Gọi I là trung điểm của BC, dựng \(OH\bot AI,H\in AI\).

Tam giác OBC cân tại O \(\Rightarrow OI\bot BC\)

Mà \(AO\bot BC\,(vi\,AO\bot \left( OBC) \right)\)

Suy ra, \(BC\bot (AOI)\Rightarrow BC\bot OH\)

Theo cách dựng, ta có: \(OH\bot AI\Rightarrow OH\bot (ABC)\) (như vậy, điểm H đã dựng thỏa mãn yêu cầu của đề bài).

Tam giác OBC vuông cân tại O \(\Rightarrow OI=\frac{BC}{2}=\frac{a\sqrt{2}}{2}\Rightarrow OI=OA=\frac{a\sqrt{2}}{2}\)

Tam giác OAI vuông cân tại O, \(\Rightarrow \frac{AO}{AI}=\sin {{45}^{0}}=\frac{1}{\sqrt{2}}\)

Ta có:

\(\begin{array}{l}\frac{{{V_{OABH}}}}{{{V_{OABI}}}} = \frac{{AH}}{{AI}} = \frac{{AH.AI}}{{A{I^2}}} = {\left( {\frac{{OA}}{{AI}}} \right)^2} = {\left( {\frac{1}{{\sqrt 2 }}} \right)^2} = \frac{1}{2}\\\,\frac{{{V_{AOBI}}}}{{{V_{OABC}}}} = \frac{{{S_{OIB}}}}{{{S_{OBC}}}} = \frac{1}{2}\\ \Rightarrow {V_{OABH}} = \frac{1}{2}.\frac{1}{2}.{V_{OABC}} = \frac{1}{2}.\frac{1}{2}.\left( {\frac{1}{3}OA.\frac{1}{2}OB.OC} \right) = \frac{1}{4}.\left( {\frac{1}{6}.\frac{{a\sqrt 2 }}{2}.a.a} \right) = \frac{{{a^3}\sqrt 2 }}{{48}}\end{array}\)

Chọn: D.