Phương pháp giải:

- Lập tỉ số thể tích \(\frac{{{V_{H.ABCD}}}}{{{V_{S.ABCD}}}} = \frac{{d(H,(ABCD))}}{{d(S,(ABCD))}} = \frac{{HK}}{{SA}}\).

- Tính thể tích \({V_{H.ABCD}}\)theo \({V_{S.ABCD}}\) .

Lời giải chi tiết:

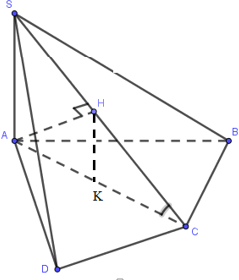
Ta có:

. \(\left\{ \begin{array}{l}SC \cap (ABCD) = C\\SA \bot (ABCD)\end{array} \right. \Rightarrow \left( {\widehat {SC,(ABCD)}} \right) = \left( {\widehat {SC,AC}} \right) = \widehat {SCA} = {60^0}\)

Tam giác SAC vuông tại A, \(AH\bot SC\), suy ra:

\(\left\{ \begin{array}{l}SA = AC.\tan \widehat {SCA} = a\sqrt 2 .\tan {60^0} = a\sqrt 6 \\\frac{{HC}}{{SC}} = \frac{{HC.SC}}{{S{C^2}}} = {\left( {\frac{{AC}}{{SC}}} \right)^2} = {\cos ^2}\widehat {SCA} = {\cos ^2}{60^0} = \frac{1}{4}\end{array} \right.\)

 Vì HK//SA nên : \(\frac{{HK}}{{SA}} = \frac{{HC}}{{SC}} = \frac{1}{4} \Rightarrow \frac{{{V_{H.ABCD}}}}{{{V_{S.ABCD}}}} = \frac{1}{4} \Rightarrow {V_{H.ABCD}} = \frac{1}{4}{V_{S.ABCD}} = \frac{1}{4}.\frac{1}{3}.SA.{S_{ABCD}} = \frac{1}{4}.\frac{1}{3}.a\sqrt 6 .\frac{3}{2}{a^2} = \frac{{{a^3}\sqrt 6 }}{8}\)

Chọn: C.