Câu hỏi
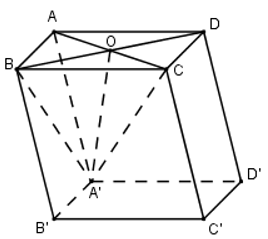
Cho khối lăng trụ \(ABCD.A’B’C’D’\) có thể tích bằng \(12\), đáy \(ABCD\) là hình vuông tâm \(O\). Thể tích khối chóp \(A’.BCO\) bằng:
- A \(1\)
- B \(4\)
- C \(3\)
- D \(2\)
Phương pháp giải:
So sánh chiều cao và diện tích đáy của khối chóp \(A’.BCO\) và khối lăng trụ \(ABCD.A’B’C’D’\).
Lời giải chi tiết:
Ta có:
\(\begin{align} & {{V}_{A'BCO}}=\frac{1}{3}d\left( A';\left( BCO \right) \right).{{S}_{BCO}}=\frac{1}{3}d\left( A';\left( ABCD \right) \right).\frac{1}{4}{{S}_{ABCD}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{12}d\left( A';\left( ABCD \right) \right).{{S}_{ABCD}}=\frac{1}{12}{{V}_{ABCD.A'B'C'D'}}=\frac{1}{12}.12=1 \\ \end{align}\)
Chọn A.