Câu hỏi
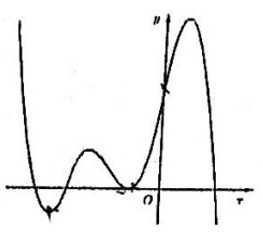
Cho hàm số \(y=f(x)\)xác định trên \(\mathbb{R}\) và có đồ thị hàm số \(y=f'(x)\) là đường cong ở hình bên. Hỏi hàm số \(y=f(x)\)có bao nhiêu điểm cực trị ?
- A 6
- B 5
- C 4
- D 3
Phương pháp giải:
Đánh giá giá trị của \(f'(x)\)và chỉ ra cực đại, cực tiểu của hàm số \(y=f(x)\):
- Cực tiểu là điểm mà tại đó \(f'(x)\) đổi dấu từ âm sang dương.
- Cực đại là điểm mà tại đó \(f'(x)\) đổi dấu từ dương sang âm.
Lời giải chi tiết:
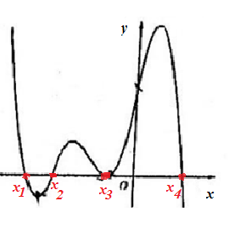
- Tại \(x={{x}_{1}}\), \(f'(x)\) đổi dấu từ dương sang âm
=> Hàm số \(y=f(x)\)đạt cực đại tại \(x={{x}_{1}}\).
- Tại \(x={{x}_{2}}\), \(f'(x)\) đổi dấu từ âm sang dương
=> Hàm số \(y=f(x)\)đạt cực tiểu tại \(x={{x}_{2}}\).
- Tại \(x={{x}_{3}}\), \(f'(x)\) không đổi dấu => Hàm số \(y=f(x)\)không đạt cực trị tại \(x={{x}_{3}}\).
- Tại \(x={{x}_{4}}\), \(f'(x)\) đổi dấu từ dương sang âm => Hàm số \(y=f(x)\)đạt cực đại tại \(x={{x}_{4}}\).
Vậy, hàm số \(y=f(x)\)có tất cả 3 cực trị.
Chọn: D.







