Lời giải chi tiết:

\(\begin{array}{l}y = {x^3} - 3{x^2} - ({m^2} - 2)x + {m^2}\\y' = 3{x^2} - 6x - {m^2} + 2\\y'' = 6x - 6\\y'' = 0 \Leftrightarrow x = 1\end{array}\)

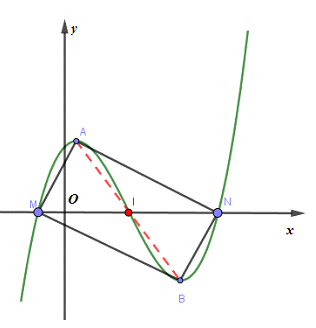
Gọi A, B là 2 điểm cực trị của (C); M, N là giao điểm của (C) với trục hoành (biểu diễn như hình vẽ).

Tâm đối xứng của (C): \(I(1;0)\in Ox\)

\(\Rightarrow \)M đối xứng N qua I.

\(\Rightarrow \)AMBN là hình bình hành. Như vậy, để AMBN là hình chữ nhật thì AB = MN. 

* Lập phương trình đường thẳng AB:

\(y={{x}^{3}}-3{{x}^{2}}-({{m}^{2}}-2)x+{{m}^{2}},\,\,y'=3{{x}^{2}}-6x-{{m}^{2}}+2\)

Chia \(y\)cho \(y'\), ta có:  \(y=\frac{1}{3}(x-1).y'-\frac{2}{3}({{m}^{2}}+1)x+\frac{2}{3}({{m}^{2}}+1)\)

\(\Rightarrow \)PT đường thẳng AB:  \(y=-\frac{2}{3}({{m}^{2}}+1)x+\frac{2}{3}({{m}^{2}}+1)\,\,(d)\)

Gọi tọa độ điểm 2 điểm A, B là:  \(A\left( {{x}_{1}};-\frac{2}{3}({{m}^{2}}+1){{x}_{1}}+\frac{2}{3}({{m}^{2}}+1) \right)\,,\,\,B\left( {{x}_{2}};-\frac{2}{3}({{m}^{2}}+1){{x}_{2}}+\frac{2}{3}({{m}^{2}}+1) \right)\)

Ta có: \(y'=0\Leftrightarrow 3{{x}^{2}}-6x-{{m}^{2}}+2=0\)

\( \Rightarrow {x_1} + {x_2} = 2,\,\,{x_1}{x_2} = \frac{{2 - {m^2}}}{3}\) 

Độ dài đoạn AB:

    \(\begin{array}{l}AB = \sqrt {{{({x_2} - {x_1})}^2} + {{\left[ {\left( { - \frac{2}{3}({m^2} + 1){x_2} + \frac{2}{3}({m^2} + 1)} \right) - \left( { - \frac{2}{3}({m^2} + 1){x_1} + \frac{2}{3}({m^2} + 1)} \right)} \right]}^2}} \\ = \sqrt {{{({x_2} - {x_1})}^2} + \frac{4}{9}{{({m^2} + 1)}^2}{{({x_2} - {x_1})}^2}}  = \sqrt {\left[ {1 + \frac{{4{{({m^2} + 1)}^2}}}{9}} \right]{{({x_2} - {x_1})}^2}}  = \sqrt {\left[ {1 + \frac{{4{{({m^2} + 1)}^2}}}{9}} \right]\left[ {{{({x_2} + {x_1})}^2} - 4{x_1}{x_2}} \right]} \\ = \sqrt {\left[ {1 + \frac{{4{{({m^2} + 1)}^2}}}{9}} \right]\left[ {{2^2} - 4.\frac{{2 - {m^2}}}{3}} \right]}  = \sqrt {\left[ {1 + \frac{{4{{({m^2} + 1)}^2}}}{9}} \right]\left[ {\frac{4}{3}({m^2} + 1)} \right]} \end{array}\)

* Xét phương trình hoành độ giao điểm của (C) với trục hoành:

\({x^3} - 3{x^2} - ({m^2} - 2)x + {m^2} = 0 \Leftrightarrow (x - 1)({x^2} - 2x - {m^2}) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x - {m^2} = 0\end{array} \right.\)

Tọa độ điểm các điểm M, N là:  \(M({{x}_{1}}';0),\,\,N({{x}_{2}}';0)\) , với \({{x}_{1}}'+{{x}_{2}}'=2,\,\,{{x}_{1}}'.{{x}_{2}}'=-{{m}^{2}}\)

               \(MN=\sqrt{{{({{x}_{2}}'-{{x}_{1}}')}^{2}}}=\sqrt{{{({{x}_{2}}'+{{x}_{1}}')}^{2}}-4{{x}_{1}}'{{x}_{2}}'}=\sqrt{{{2}^{2}}-4.(-{{m}^{2}})}=\sqrt{4({{m}^{2}}+1)}\)

\(\begin{array}{l}AB{\rm{ }} = {\rm{ }}MN \Leftrightarrow \sqrt {\left[ {1 + \frac{{4{{({m^2} + 1)}^2}}}{9}} \right]\left[ {\frac{4}{3}({m^2} + 1)} \right]}  = \sqrt {4({m^2} + 1)}  \Leftrightarrow \left[ {1 + \frac{{4{{({m^2} + 1)}^2}}}{9}} \right]\left[ {\frac{4}{3}({m^2} + 1)} \right] = 4({m^2} + 1)\\ \Leftrightarrow 1 + \frac{{4{{({m^2} + 1)}^2}}}{9} = 3 \Leftrightarrow \frac{{4{{({m^2} + 1)}^2}}}{9} = 2 \Leftrightarrow {({m^2} + 1)^2} = \frac{9}{2} \Leftrightarrow 2{m^4} + 4{m^2} - 7 = 0 \Leftrightarrow \left[ \begin{array}{l}{m^2} = \frac{{ - 2 + 3\sqrt 2 }}{2}\\{m^2} = \frac{{ - 2 - 3\sqrt 2 }}{2}\,\,(vo\,\,nghiem)\end{array} \right.\end{array}\) \(T = m_1^4 + m_2^4 = 2.{\left( {\frac{{ - 2 + 3\sqrt 2 }}{2}} \right)^2} = 11 - 6\sqrt 2 \)

Chọn: B.