Lời giải chi tiết:

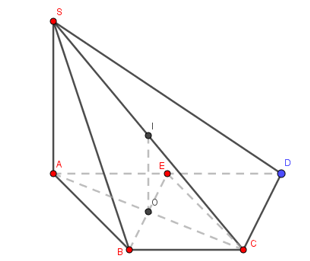
Gọi O là giao điểm của AC và BE, I là trung điểm của SC.

* Ta sẽ chứng minh: I là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCE\).

Tứ giác ABCE có: \(BC//AE,\,BC=AE\Rightarrow ABCE:\) hình bình hành, mà \(AB=BC,\,\,\widehat{ABC}={{90}^{0}}\Rightarrow ABCE:\)hình vuông.

\(O=AC\cap BE\Rightarrow O\) là tâm của hình vuông ABCE.

Ta có:

OI là đường trung bình của tam giác SAC \(\Rightarrow OI//SA\)

Mà \(SA\bot (ABCD)\Rightarrow OI\bot (ABCD)\Rightarrow IA=IB=IC=ID\)

I là trung điểm của SA \(\Rightarrow IS=IA=IB=IC=ID\)

Vậy I là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCE\).

* Bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCE\):

\(R=\frac{SC}{2}=\frac{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}{2}=\frac{\sqrt{{{(a\sqrt{2})}^{2}}+{{(a\sqrt{2})}^{2}}}}{2}=a\)

Chọn: D.