Phương pháp giải:

Sử dụng phương pháp tọa độ trong không gian.

Lời giải chi tiết:

Gắn hình chóp vào hệ trục tọa độ Oxyz (như hình vẽ).

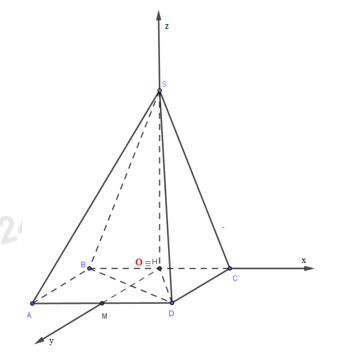
Ta có:

\(\begin{array}{l}H \equiv O(0;0;0),\,\,B( - \frac{{a\sqrt 2 }}{2};0;0),\,\,\\S(0;0;\frac{{a\sqrt 2 }}{2}),\,\,D(\frac{{a\sqrt 2 }}{2};a;0)\end{array}\)

Gọi \(I\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)\)là tâm mặt cầu ngoại tiếp hình chóp \(S.BHD.\)

\( \Leftrightarrow \left\{ \begin{array}{l}I{H^2} = I{S^2}\\I{H^2} = I{B^2}\\I{H^2} = I{D^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0}^2 + {y_0}^2 + {z_0}^2 = {x_0}^2 + {y_0}^2 + {\left( {{z_0} - \frac{{a\sqrt 2 }}{2}} \right)^2}\\{x_0}^2 + {y_0}^2 + {z_0}^2 = {\left( {{x_0} + \frac{{a\sqrt 2 }}{2}} \right)^2} + {y_0}^2 + {z_0}^2\\{x_0}^2 + {y_0}^2 + {z_0}^2 = {\left( {{x_0} - \frac{{a\sqrt 2 }}{2}} \right)^2} + {\left( {{y_0} - a} \right)^2} + {z_0}^2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{z_0}a\sqrt 2  - \frac{{{a^2}}}{2} = 0\\{x_0}a\sqrt 2  + \frac{{{a^2}}}{2} = 0\\ - {x_0}a\sqrt 2  - 2a{y_0} + \frac{3}{2}{a^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} =  - \frac{{a\sqrt 2 }}{4}\\{y_0} = a\\{z_0} = \frac{{a\sqrt 2 }}{4}\end{array} \right.\)

Bán kính mặt cầu:

        \(R=IH=\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}+{{z}_{0}}^{2}}=\sqrt{{{\left( -\frac{a\sqrt{2}}{4} \right)}^{2}}+{{\left( a \right)}^{2}}+{{\left( \frac{a\sqrt{2}}{4} \right)}^{2}}}=a\sqrt{\frac{1}{8}+1+\frac{1}{8}}=\frac{a\sqrt{5}}{2}\)

Chọn: B.