Câu hỏi
Cho hình cầu đường kính \(2a\sqrt{3}\). Mặt phẳng (P) cắt hình cầu theo thiết diện là hình tròn có bán kính bằng\(a\sqrt{2}\). Tính khoảng cách từ tâm hình cầu đến mặt phẳng (P).
- A \(a.\)
- B \(\frac{a}{2}.\)
- C \(a\sqrt{10}.\)
- D \(\frac{a\sqrt{10}}{2}.\)
Phương pháp giải:
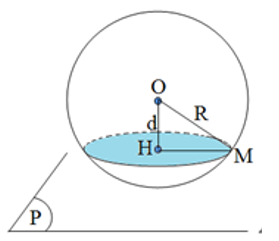
\({{d}^{2}}+{{r}^{2}}={{R}^{2}}\)
Trong đó, \(d\): khoảng cách từ tâm O đến mặt phẳng (P),
\(r\): bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P),
\(R\): bán kính hình cầu.
Lời giải chi tiết:
\({{d}^{2}}+{{r}^{2}}={{R}^{2}}\Leftrightarrow {{d}^{2}}+{{\left( a\sqrt{2} \right)}^{2}}={{\left( \frac{2a\sqrt{3}}{2} \right)}^{2}}\Leftrightarrow d=a.\)
Chọn: A.
Câu hỏi trước
