Phương pháp giải:

- Sử dụng phương pháp hàm số để tìm GTNN của diện tích xung quanh của lăng trụ tứ giác đều có thể tích không đổi.

- Từ đó, tính số tiền tối thiểu phải trả: \({{t}_{\min }}={{S}_{k\,Min}}\times 600\,\,000\), trong đó \({{S}_{k\,Min}}\) là diện tích tối thiểu của phần làm bằng kính.

Lời giải chi tiết:

Gọi \(a,\,\,h,\,\,\left( a,h>0 \right)\)lần lượt là độ dài cạnh đáy và chiều cao của lăng trụ (m).

Khi đó, \(V={{S}_{d}}.h={{a}^{2}}h=8\,({{m}^{3}})\,\,\Rightarrow h=\frac{8}{{{a}^{2}}}\)

\({{S}_{k}}={{S}_{xq}}+{{S}_{d}}=4ah+{{a}^{2}}=4a.\frac{8}{{{a}^{2}}}+{{a}^{2}}=\frac{32}{a}+{{a}^{2}}.\)

Xét hàm số \(y=f(a)=\frac{32}{a}+{{a}^{2}}\):

\(f'(a)=-\frac{32}{{{a}^{2}}}+2a,\,\,f'(a)=0\Leftrightarrow -\frac{32}{{{a}^{2}}}+2a=0\Leftrightarrow {{a}^{3}}=16\Leftrightarrow a=\sqrt[3]{16}\)

Bảng biến thiên

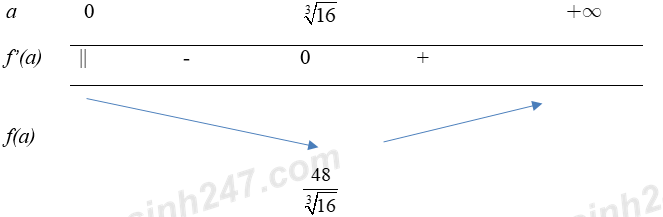
 \(\begin{array}{l} \Rightarrow {S_{k\,Min}} = \frac{{48}}{{\sqrt[3]{{16}}}} \approx 19\\ \Rightarrow {t_{\min }} \approx 19 \times 600\,000 = 11400\,000\end{array}\)

Chọn: A.