Câu hỏi
Cho hàm số \(y=f(x)\)xác định và liên tục trên các khoảng \(\left( -\infty ;\frac{1}{2} \right)\) và \(\left( \frac{1}{2};+\infty \right)\). Đồ thị hàm số \(y=f(x)\)là đường cong trong hình bên.
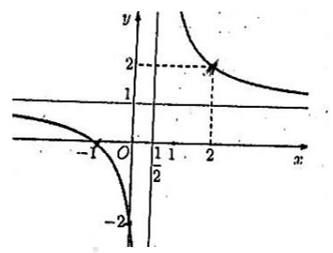
Tìm mệnh đề đúng trong các mệnh đề sau.
- A \(\underset{\left[ 1;2 \right]}{\mathop{\max }}\,f(x)=2.\)
- B \(\underset{\left[ -2;-1 \right]}{\mathop{\max }}\,f(x)=0.\)
- C \(\underset{\left[ -3;0 \right]}{\mathop{\max }}\,f(x)=f(-3).\)
- D \(\underset{\left[ 3;4 \right]}{\mathop{\max }}\,f(x)=f(4).\)
Lời giải chi tiết:
\(\underset{\left[ 1;2 \right]}{\mathop{\max }}\,f(x)=f(1)>2\Rightarrow \)Đáp án A sai.
\(\underset{\left[ -2;-1 \right]}{\mathop{\max }}\,f(x)=f(-2)>0\Rightarrow \)Đáp án B sai.
\(\underset{\left[ -3;0 \right]}{\mathop{\max }}\,f(x)=f(-3)\Rightarrow \)Đáp án C đúng.
\(\underset{\left[ 3;4 \right]}{\mathop{\max }}\,f(x)=f(3)>f(4)\Rightarrow \)Đáp án D sai.
Chọn: C.
Câu hỏi trước
