Câu hỏi
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(C\), mặt bên \(SAC\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(I\) là trung điểm của \(SC\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I) \(AI\bot SC.\).
(II) \(\left( SBC \right)\bot \left( SAC \right).\)
(III) \(AI\bot BC.\)
(IV) \(\left( ABI \right)\bot \left( SBC \right).\)
- A
1
- B 2
- C
3
- D 4
Phương pháp giải:
Sử dụng các định lí về hai mặt phẳng vuông góc
Lời giải chi tiết:
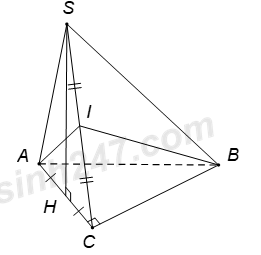
Tam giác \(SAC\) đều có \(I\) là trung điểm của \(SC\) nên \(AI\bot SC\).
\(\Rightarrow \) (I) đúng.
Gọi \(H\) là trung điểm \(AC\) suy ra \(SH\bot AC\). Mà \(\left( SAC \right)\bot \left( ABC \right)\) theo giao tuyến \(AC\) nên \(SH\bot \left( ABC \right)\) do đó \(SH\bot BC\). Hơn nữa theo giả thiết tam giác \(ABC\) vuông tại \(C\) nên \(BC\bot AC\).
Từ đó suy ra \(BC\bot \left( SAC \right)\Rightarrow BC\bot AI.\) Do đó đáp án (III) đúng.
Từ mệnh đề (I) và (III) suy ra mệnh đề (IV) đúng.
Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AC\\BC \bot AH\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right)\\BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAC} \right)\end{array}\).
Suy ra (II) đúng.
Vậy cả 4 mệnh đề trên đều đúng.
Chọn D.







