Phương pháp giải:

Đưa phương trình về dạng \(f\left( x \right)=m\), số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) và đường thẳng y = m.

Lời giải chi tiết:

Ta có \(\sqrt{{{x}^{2}}+1}\ne 0\,\,\forall x\in R\Rightarrow m=\frac{x+1}{\sqrt{{{x}^{2}}+1}}=f\left( x \right)\)

Xét hàm số \(y=f\left( x \right)\) có TXĐ: D = R.

\(f'\left( x \right)=\frac{\sqrt{{{x}^{2}}+1}-\left( x+1 \right)\frac{x}{\sqrt{{{x}^{2}}+1}}}{{{\left( \sqrt{{{x}^{2}}+1} \right)}^{2}}}=\frac{1-x}{{{\left( \sqrt{{{x}^{2}}+1} \right)}^{3}}}=0\Leftrightarrow x=1\)

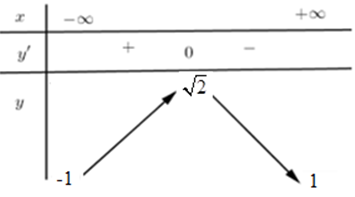
Bảng biến thiên:

Quan sát bảng biến thiên ta thấy: đường thẳng \(y=m\) cắt đồ thị hàm số tại 2 điểm phân biệt \(\Leftrightarrow 1<m<\sqrt{2}\)

Trong khoảng \(\left( 1;\sqrt{2} \right)\) không có số nguyên nào.

Chọn C.