Câu hỏi
Cho hàm số \(y=\sqrt{{{x}^{2}}-2x}.\) Mệnh đề nào sau đây đúng?
- A Hàm số có một điểm cực trị.
- B Hàm số đồng biến trên các khoảng xác định của nó.
- C Hàm số nghịch biến trên khoảng \(\left( -\infty ;\,\,0 \right).\)
- D Hàm số đồng biến trên khoảng \(\left( 1;+\infty \right).\)
Phương pháp giải:
Khảo sát sự biến thiên của hàm số sau đó đưa ra kết luận đúng.
Lời giải chi tiết:
ĐK: \({{x}^{2}}-2x\ge 0\Leftrightarrow \left[ \begin{align} & x\le 0 \\ & x\ge 2 \\ \end{align} \right.\Rightarrow D=\left( -\infty ;0 \right)\cup \left( 2;+\infty \right).\)
Có \(y'=\frac{2x-2}{2\sqrt{{{x}^{2}}-2x}}=\frac{x-1}{\sqrt{{{x}^{2}}-2x}}\Rightarrow y'=0\Leftrightarrow x=1.\)
Ta có BBT:
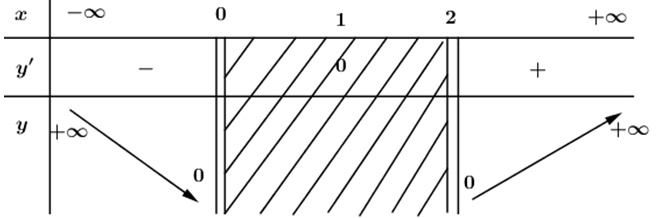
Dựa vào BBT ta thấy đáp án C đúng.
Chọn C.
Câu hỏi trước
