Phương pháp giải:

+) Xác định mặt phẳng chia tứ diện.

+) Sử dụng công thức tỉ lệ thể tích để tính tỉ lệ thể tích hai phần được chia.

Lời giải chi tiết:

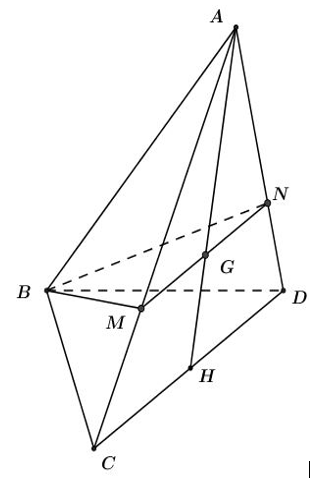
Gọi H là trung điểm của CD.  Ta có G là trọng tâm tam giác ACD \(\Rightarrow \frac{AG}{AH}=\frac{2}{3}.\)

Trong mặt phẳng ACD, qua G kẻ đường thẳng song song với CD,

cắt AC tại M và cắt AD tại N.

Khi đó ta có mặt phẳng (P) là mặt phẳng (BMN).

Mặt phẳng (BMN) chia tứ diện ABCD thành hai phần là ABMN có thể tích

\({{V}_{1}}\) và BMNDC có thể tích \({{V}_{2}}.\)

\(\Rightarrow V={{V}_{ABCD}}={{V}_{1}}+{{V}_{2}}.\)

Ta có MN//CD theo cách dựng \(\Rightarrow \frac{AM}{AC}=\frac{AN}{AD}=\frac{AG}{AH}=\frac{2}{3}\) (định lý Ta-lét).

Theo công thức tỉ lệ thể tích ta có: \(\frac{{{V}_{ABMN}}}{{{V}_{ABCD}}}=\frac{{{V}_{1}}}{V}=\frac{AB}{AB}.\frac{AM}{AC}.\frac{AN}{AD}=\frac{2}{3}.\frac{2}{3}=\frac{4}{9}.\)

\(\begin{align}  & \Rightarrow {{V}_{1}}=\frac{4}{9}V\Rightarrow {{V}_{2}}=V-{{V}_{1}}=\frac{5}{9}V. \\  & \Rightarrow {{V}_{1}}<{{V}_{2}}\Rightarrow \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{4}{9}.\frac{9}{5}=\frac{4}{5}. \\ \end{align}\)

Chọn D.