Câu hỏi
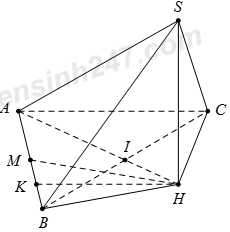
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A với AB = AC = a. Gọi M là trung điểm của cạnh AB, hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABC) trùng với tâm đường tròn ngoại tiếp tam giác BMC. Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng \({60^0}.\) Tính độ dài SB.
- A \(\frac{{a\sqrt {10} }}{2}.\)
- B \(\frac{{a\sqrt {30} }}{6}.\)
- C \(\frac{{a\sqrt {10} }}{4}.\)
- D \(\frac{{a\sqrt {30} }}{4}.\)
Phương pháp giải:
Áp dụng phương pháp tìm góc giữa đường thẳng và mặt phẳng – hệ thức lượng trong tam giác vuông để giải quyết yêu cầu của bài toán
Lời giải chi tiết:
Gọi I là trung điểm của \(BC \Rightarrow AI\) là đường trung trực của BC.
Gọi K là trung điểm của MB, vẽ đường thẳng qua K và vuông góc với MB cắt AI tại H.
Suy ra KH là đường trung trực của MB và H là tâm đường tròn ngoại tiếp tam giác MBC. Do đó \(SH \bot \left( {ABCD} \right).\)
Ta có HB là hình chiếu vuông góc của SB trên mp(ABC).
Suy ra \(\widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;BH} \right)} = \widehat {SBH} = {60^0}.\)
Tam giác AKH vuông cân tại K\( \Rightarrow \,\,HK = AK = \frac{3}{4}AB = \frac{{3a}}{4}.\)
Tam giác BKH vuông tại K có \(BH = \sqrt {B{K^2} + H{K^2}} = \sqrt {\frac{{{a^2}}}{{16}} + \frac{{9{a^2}}}{{16}}} = \frac{{a\sqrt {10} }}{4}.\)
Tam giác SBH vuông tại H, có \(\cos \widehat {SBH} = \frac{{BH}}{{SB}} \Rightarrow SB = \frac{{a\sqrt {10} }}{4}:\cos {60^0} = \frac{{a\sqrt {10} }}{2}.\)
Chọn A.