Câu hỏi
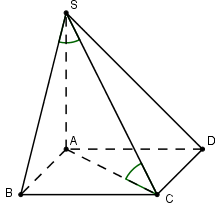
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, BC = a. Cạnh bên SA vuông góc với mặt phẳng đáy, đường thẳng SC tạo với các mặt phẳng (SAB) và (ABCD) các góc đều bằng \({30^0}.\) Tính diện tích S của hình chữ nhật ABCD.
- A \(S = {a^2}\sqrt 3 .\)
- B \(S = 2{a^2}.\)
- C \(S = {a^2}\sqrt 2 .\)
- D \(S = {a^2}.\)
Phương pháp giải:
Áp dụng phương pháp tìm góc giữa đường thẳng và mặt phẳng – hệ thức lượng trong tam giác vuông để giải quyết yêu cầu của bài toán
Lời giải chi tiết:
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow \,\,AC\) là hình chiếu vuông góc của SC trên (ABCD)
\( \Rightarrow \) Góc giữa đường thẳng SC và mặt phẳng (ABCD) là \(\widehat {SCA} = {30^0}.\)
Ta có \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow \,\,BC \bot \left( {SAB} \right)\,\, \Rightarrow \,\,SB\) là hình chiếu vuông góc của SC trên (SAB).
\( \Rightarrow \) Góc giữa đường thẳng SC và mặt phẳng (SAB) là \(\widehat {BSC} = {30^0}.\)
Đặt \(AB = x\,\, \Rightarrow \,\,AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{x^2} + {a^2}} \,\, \Rightarrow \,\,\left\{ \begin{array}{l}SA = AC.\tan \widehat {SCA} = \sqrt {\frac{{{x^2} + {a^2}}}{3}} \\SB = \frac{{BC}}{{\tan \widehat {BSC}}} = a\sqrt 3\end{array} \right.\)
Tam giác SAB vuông tại \(A\,\, \Rightarrow \,\,S{A^2} + A{B^2} = S{B^2}\)\( \Leftrightarrow \,\,\frac{{{x^2} + {a^2}}}{3} + {x^2} = 3{a^2} \Leftrightarrow \frac{4}{3}{x^2} = \frac{8}{3}{a^2} \Leftrightarrow x = a\sqrt 2 .\)
Vậy diện tích hình chữ nhật ABCD là \(S = AB\,\, \times \,BC = {a^2}\sqrt 2 .\)
Chọn C.