Phương pháp giải:

Áp dụng công thức tỉ số thể tích: Cho chóp tam giác S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’ ta có \(\frac{{{V}_{S.A'B'C'}}}{{{V}_{S.ABC}}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}\)

Lời giải chi tiết:

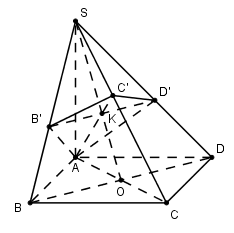
Gọi \(O=AC\cap BD\), trong (SBD) gọi \(K=B'D'\cap SO\), trong (SAC) gọi \(C'=AK\cap SC\Leftrightarrow SC\cap \left( AB'D' \right)=C'\)

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot AB'\\\left\{ \begin{array}{l}AB' \bot BC\\AB' \bot SB\end{array} \right. \Rightarrow AB' \bot \left( {SBC} \right) \Rightarrow AB' \bot SC\end{array}\)

Tương tự ta chứng minh được \(AD'\bot SC\Rightarrow SC\bot \left( AB'C'D' \right)\Rightarrow AC'\bot SC\)

Xét tam giác vuông  SAB ta có \(\frac{SB'}{SB}=\frac{S{{A}^{2}}}{S{{B}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{B}^{2}}}=\frac{4{{a}^{2}}}{4{{a}^{2}}+{{a}^{2}}}=\frac{4}{5}\)

Xét tam giác vuông SAD ta có \(\frac{SD'}{SD}=\frac{S{{A}^{2}}}{S{{D}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{D}^{2}}}=\frac{4{{a}^{2}}}{4{{a}^{2}}+{{a}^{2}}}=\frac{4}{5}\)

Ta có: \(A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}=2{{a}^{2}}\)

Xét tam giác vuông SAC ta có \(\frac{SC'}{SC}=\frac{S{{A}^{2}}}{S{{C}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{C}^{2}}}=\frac{4{{a}^{2}}}{4{{a}^{2}}+2{{a}^{2}}}=\frac{2}{3}\)

Ta có

\(\begin{array}{l}\frac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}} = \frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}} = \frac{4}{5}.\frac{2}{3} = \frac{8}{{15}} \Rightarrow {V_{S.AB'C'}} = \frac{8}{{15}}{V_{S.ABC}} = \frac{4}{{15}}{V_{S.ABCD}}\\\frac{{{V_{S.AC'D'}}}}{{{V_{S.ACD}}}} = \frac{{SC'}}{{SC}}.\frac{{SD'}}{{SD}} = \frac{2}{3}.\frac{4}{5} = \frac{8}{{15}} \Rightarrow {V_{S.AC'D'}} = \frac{8}{{15}}{V_{S.ACD}} = \frac{4}{{15}}{V_{S.ABCD}}\\ \Rightarrow {V_{S.AB'C'D'}} = \frac{8}{{15}}{V_{S.ABCD}}\end{array}\)

Mà \({{V}_{S.ABCD}}=\frac{1}{3}SA.{{S}_{ABCD}}=\frac{1}{3}2a.{{a}^{2}}=\frac{2}{3}{{a}^{3}}\Rightarrow {{V}_{S.AB'C'D'}}=\frac{8}{15}.\frac{1}{3}{{a}^{3}}=\frac{16{{a}^{3}}}{45}\)

Chọn C.