Câu hỏi
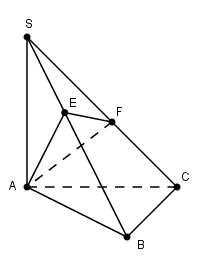
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a. Biết SA = a và \(SA\bot \left( ABC \right)\). Gọi E, F lần lượt là hình chiếu của A trên SB và SC. Tính thể tích khối chóp S.AEF.
- A \(\frac{{{a}^{3}}}{18}\)
- B \(\frac{{{a}^{3}}}{12}\)
- C \(\frac{{{a}^{3}}}{36}\)
- D \(\frac{{{a}^{3}}}{24}\)
Phương pháp giải:
Áp dụng công thức tỉ số thể tích: Cho chóp tam giác S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’ ta có \(\frac{{{V}_{S.A'B'C'}}}{{{V}_{S.ABC}}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}\)
Lời giải chi tiết:
\(\Delta ABC\)vuông cân tại B \(\Rightarrow BA=BC=a,AC=BC\sqrt{2}=a\sqrt{2}\)
Xét tam giác vuông SAB có \(\frac{SE}{SB}=\frac{S{{A}^{2}}}{S{{B}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{B}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}+{{a}^{2}}}=\frac{1}{2}\)
Xét tam giác vuông SAC có \(\frac{SF}{SC}=\frac{S{{A}^{2}}}{S{{C}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{C}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}+2{{a}^{2}}}=\frac{1}{3}\)
\(\Rightarrow \frac{{{V}_{S.AEF}}}{{{V}_{S.ABC}}}=\frac{SE}{SB}.\frac{SF}{SC}=\frac{1}{2}.\frac{1}{3}=\frac{1}{6}\Rightarrow {{V}_{S.AEF}}=\frac{1}{6}{{V}_{S.ABC}}=\frac{1}{6}.\frac{1}{3}SA.\frac{1}{2}BA.BC=\frac{1}{36}.a.{{a}^{2}}=\frac{{{a}^{3}}}{36}\)
Chọn C