Câu hỏi
Bảng biến thiên sau đây là của hàm số nào?
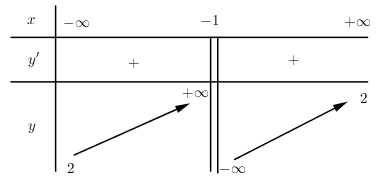
- A \(y=\frac{2x+1}{x+1}\)
- B \(y=\frac{x-1}{2x+1}\)
- C \(y=\frac{x+2}{1+x}\)
- D \(y=\frac{2x+1}{x-1}\)
Phương pháp giải:
Dựa vào đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số.
\(\underset{x\to -\infty }{\mathop{\lim }}\,y=a\) hoặc \(\underset{x\to +\infty }{\mathop{\lim }}\,y=a\) thì y = a là đường tiệm cận ngang của đồ thị hàm số.
\(\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,y=\pm \infty \Rightarrow x={{x}_{0}}\) là tiệm cận đứng của đồ thị hàm số.
Lời giải chi tiết:
Ta có \(\underset{x\to -1}{\mathop{\lim }}\,y=\infty \Rightarrow \) Đồ thị hàm số có tiệm cận đứng là \(x=-1\Rightarrow \) Loại đáp án B và D.
\(\underset{x\to \pm \infty }{\mathop{\lim }}\,y=2\Rightarrow \) Đồ thị hàm số có tiệm cận ngang là y = 2 \(\Rightarrow \) Loại đáp án C.
Chọn A.







