Câu hỏi
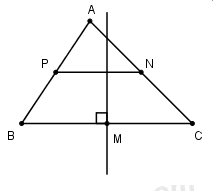
Cho tam giác ABC, biết \(M\left( {2;2} \right),N\left( {1;3} \right),P\left( {3;0} \right)\) lần lượt là trung điểm của BC, AC, AB. Đường trung trực của đoạn thẳng BC có phương trình:
- A \(x - 2y + 5 = 0\)
- B x - y - 3 = 0
- C \(2x - 3y + 2 = 0\)
- D \(3x + 2y - 10 = 0\)
Phương pháp giải:
+) Đường trung trực của BC là đường thẳng đi qua M và vuông góc với NP.
+) Phương trình tổng quát của đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\) và có VTPT là \(\overrightarrow n \left( {a;b} \right)\,\,\left( {{a^2} + {b^2} > 0} \right)\) là: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)
Lời giải chi tiết:
Goi d là đường trung trực của BC.
NP là đường trung bình của tam giác ABC \( \Rightarrow NP//BC \Rightarrow d \bot NP\)
Ta có \(\overrightarrow {NP} = \left( {2; - 3} \right) \Rightarrow \) Đường thẳng d đi qua M và nhận \(\overrightarrow {NP} = \left( {2; - 3} \right)\) là 1 VTPT, khi đó phương trình tổng quát của đường thẳng d là: \(2\left( {x - 2} \right) - 3\left( {y - 2} \right) = 0 \Leftrightarrow 2x - 3y + 2 = 0\)
Chọn C.