Câu hỏi
Cho hàm số \(f\left( x \right)\) có đạo hàm là \({f}'\left( x \right)\). Đồ thị của hàm số \(y={f}'\left( x \right)\) như hình vẽ bên.
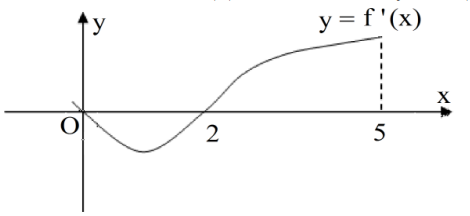
Biết \(f\left( 0 \right)+f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right)\). Giá trị nhỏ nhất, giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ 0;5 \right]\) lần lượt là:
- A \(f\left( 1 \right),f\left( 5 \right)\).
- B \(f\left( 2 \right),f\left( 0 \right)\).
- C \(f\left( 2 \right),f\left( 5 \right)\).
- D \(f\left( 0 \right),f\left( 5 \right)\).
Phương pháp giải:
Sử dụng đồ thị của hàm số \(y={f}'\left( x \right)\) ta tìm ra các khoảng đồng biến, nghịch biến và điểm gián đoạn của \(y={f}'\left( x \right)\)trên đoạn [0;5]. Vẽ BBT của \(y=f\left( x \right)\) và kết luận.
Lời giải chi tiết:
Từ đồ thị hàm số \(y={f}'\left( x \right)\) ta có \({f}'\left( x \right)<0\) trên khoảng \(\left( 0;2 \right)\), \({f}'\left( x \right)>0\) trên khoảng \(\left( 2;3 \right);\left( 3;5 \right)\) và \({f}'\left( x \right)\) gián đoạn tại \(x=3\).
Ta có BBT của hàm \(y=f\left( x \right)\) như sau:
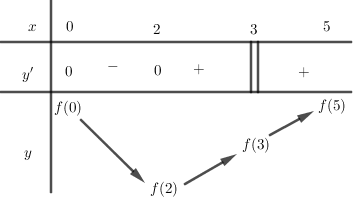
Từ BBT ta thấy giá trị nhỏ nhất của \(y=f\left( x \right)\) trên đoạn \(\left[ 0;5 \right]\) là \(f\left( 2 \right)\).
Theo giả thiết \(f\left( 0 \right)+f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right)\) mà \(f\left( 2 \right)<f\left( 3 \right)\)\(\Rightarrow f\left( 0 \right)<f\left( 5 \right)\).
Vậy giá trị lớn nhất của \(y=f\left( x \right)\) trên đoạn \(\left[ 0;5 \right]\) là \(f\left( 5 \right)\).
Chọn C.







