Câu hỏi
Cho hình chóp S.ABC có \(\widehat{BSC}={{120}^{0}},\,\,\widehat{CSA}={{60}^{0}},\,\,\widehat{ASB}={{90}^{0}}\) và SA = SB = SC. Gọi I là hình chiếu vuông góc của S trên mặt phẳng (ABC), khi đó
- A I là trung điểm của cạnh AB.
- B I là trọng tâm của tam giác ABC.
- C I là trung điểm của cạnh AC.
- D I là trung điểm của cạnh BC.
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng
Lời giải chi tiết:
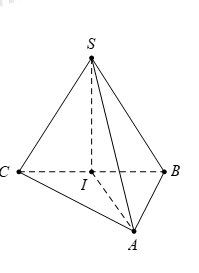
Đặt SA = a Tam giác SAB vuông cân tại S, có \(AB=\sqrt{S{{A}^{2}}+S{{B}^{2}}}=a\sqrt{2}.\)
Tam giác SAC cân tại S, có \(\widehat{CSA}={{60}^{0}}\) suy ra SA = SC = AC = a.
Áp dụng định lí Cosin cho tam giác SBC, ta có
\(B{{C}^{2}}=S{{B}^{2}}+S{{C}^{2}}-2.SB.SC.\cos \widehat{BSC}\)
\(\Rightarrow \,\,B{{C}^{2}}={{a}^{2}}+{{a}^{2}}-2{{a}^{2}}.\cos {{120}^{0}}=3{{a}^{2}}\Rightarrow \,\,\,BC=a\sqrt{3}=\sqrt{A{{B}^{2}}+A{{C}^{2}}}.\)
Khi đó, tam giác ABC vuông tại A mà I là hình chiếu của S trên mp(ABC).
Suy ra I là tâm đường tròn ngoại tiếp tam giác ABC hay chính là trung điểm BC.
Chọn D.







