Phương pháp giải:

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng

Lời giải chi tiết:

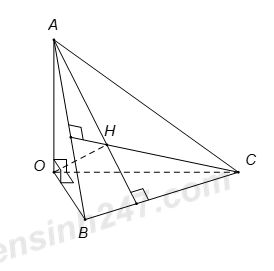
= \(\left\{ {\begin{array}{*{20}{l}}{OA \bot OB}\\{OA \bot OC}\end{array}} \right. \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC.\) Do đó A đúng.                                  

= Gọi \(I=AH\cap BC.\,\,\,\,\left( 1 \right)\)

Theo giả thiết ta có \(OH\bot \left( ABC \right)\Rightarrow OH\bot BC.\)               \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(BC\bot \left( AOI \right)\Rightarrow BC\bot OI.\)

Tam giác vuông \(BOC,\) ta có \(\frac{1}{O{{I}^{2}}}=\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}.\)

Tam giác vuông \(AOI,\) ta có \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{I}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}.\) Do đó B đúng.

= Từ chứng minh trên \(BC\bot \left( AOI \right)\Rightarrow BC\bot AI.\)           \(\left( 3 \right)\)

Gọi \(J=BH\cap AC.\) Chứng minh tương tự ta có \(AC\bot BJ\).    \(\left( 4 \right)\)

Từ \(\left( 3 \right)\) và \(\left( 4 \right)\), suy ra H là trực tâm \(\Delta ABC.\) Do đó C đúng.

Vậy D là đáp án sai.

Chọn D