Câu hỏi
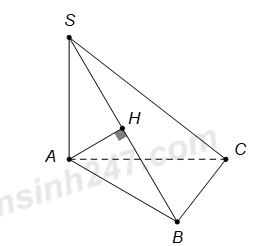
Cho hình chóp S.ABC có đáy ABC vuông tại B, cạnh bên SA vuông góc với đáy. Gọi H là chân đường cao kẻ từ A của tam giác SAB. Khẳng định nào dưới đây là sai ?
- A \(SA\bot BC.\)
- B \(AH\bot BC.\)
- C \(AH\bot AC.\)
- D \(AH\bot SC.\)
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng
Lời giải chi tiết:
Theo bài ra, ta có \(SA\bot \left( ABC \right)\) mà \(BC\subset \left( ABC \right)\Rightarrow SA\bot BC.\)
Tam giác ABC vuông tại B, có \(AB\bot BC\)\(\Rightarrow \)\(BC\bot \left( SAB \right)\Rightarrow BC\bot AH.\)
Khi đó \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC.\)
Nếu \(AH\bot AC\) mà \(SA\bot AC\) suy ra \(AC\bot \left( SAH \right)\Rightarrow AC\bot AB\) (vô lý).
Chọn C
Câu hỏi trước
