Câu hỏi
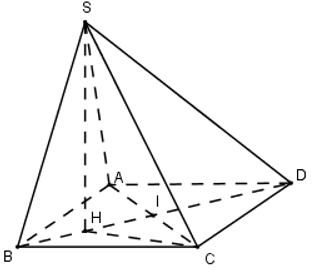
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc \(\widehat{BAD}\) bằng 600, gọi I là giao điểm của AC và BD. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm H của BI. Góc giữa SC và (ABCD) bằng 450. Thể tích của khối chóp S.ABCD bằng:
- A \(\frac{{{a}^{3}}\sqrt{39}}{12}\)
- B \(\frac{{{a}^{3}}\sqrt{39}}{24}\)
- C \(\frac{{{a}^{3}}\sqrt{39}}{8}\)
- D \(\frac{{{a}^{3}}\sqrt{39}}{48}\)
Phương pháp giải:
+) Xác định góc giữa SC và mặt đáy là góc \(\widehat{SCH}\)
+) Tính đường cao SH.
+) Tính diện tích đáy ABCD.
+) Tính thể tích \(V=\frac{1}{3}Sh\)
Lời giải chi tiết:
Tam giác ABD đều cạnh a nên BD = a \(\Rightarrow HI=\frac{a}{4}\) và \(AI=\frac{a\sqrt{3}}{2}\Rightarrow AI=IC=\frac{a\sqrt{3}}{2}\)
Xét tam giác vuông IHC có \(HC=\sqrt{I{{C}^{2}}+I{{H}^{2}}}=\sqrt{\frac{3{{a}^{2}}}{4}+\frac{{{a}^{2}}}{16}}=\frac{a\sqrt{13}}{4}\)
\(SH\bot \left( ABCD \right)\Rightarrow \widehat{\left( SC;\left( ABCD \right) \right)}=\widehat{\left( SC;HC \right)}=\widehat{SCH}={{45}^{0}}.\)
\(\Rightarrow \Delta SHC\) vuông cân tại H \(\Rightarrow SH=HC=\frac{a\sqrt{13}}{4}\)
\({{S}_{ABCD}}=\frac{1}{2}AC.BD=\frac{1}{2}a\sqrt{3}.a=\frac{{{a}^{2}}\sqrt{3}}{2}\)
Vậy \({{V}_{S.ABCD}}=\frac{1}{3}.SH.{{S}_{ABCD}}=\frac{1}{3}\frac{a\sqrt{13}}{4}.\frac{{{a}^{2}}\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{39}}{24}\)
Chọn B.