Phương pháp giải:

+) Mở rộng mặt phẳng (MDC’) rồi xác định thiết diện của hình hộp chữ nhật bị cắt bởi mặt phẳng (MDC’), từ đó phân chia thành hai phần đa diện chứa C và A’.

+) Sử dụng phân chia thể tích để phân chia khối đa diện chứa C thành hai khối chóp. Tính thể tích hai khối chóp đó theo công thức \(V=\frac{1}{3}h.S\) với h là chiều cao hình chóp và S là diện tích đáy.

+) Từ đó suy ra thể tích của phần đa diện chứa C theo thể tích V của khối hộp chữ nhật sau đó ta tính được thể tích phần đa diện chứa A’ và suy ra tỉ lệ thể tích.

Lời giải chi tiết:

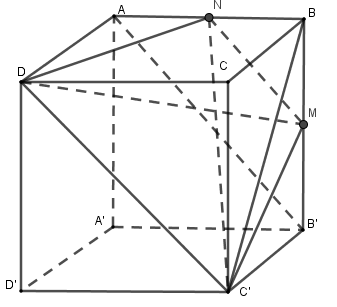
+) Bước 1: Mở rộng mặt phẳng (MDC’).

Lấy N là trung điểm của AB thì MN//AB’ (vì MN là đường trung bình của tam giác ABB’)

Mà DAB’C’ là hình bình hành nên DC’//AB’ nên suy ra MN//DC’ hay mặt phẳng (MDC’) trùng với mặt phẳng (MC’DN).

Từ đó mặt phẳng (MC’DN) chia hình hộp chữ nhật ra thành hai phần: phần đa diện chứa C là: BCC’DNM, phần đa diện chứa A’ là NMC’DD’A’AB’.

+) Bước 2: Ta có

\({{V}_{BC{C}'DNM}}={{V}_{{C}'.CDNB}}+{{V}_{N.BM{C}'}}\).

Gọi thể tích ABCD.A’B’C’D’ là V.

Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên \({C}'C\bot \left( CDNB \right),NB\bot \left( BN{C}' \right)\).

Từ đó \({{V}_{{C}'.CBND}}=\frac{1}{3}C{C}'.{{S}_{BNDC}}=\frac{1}{3}C{C}'.\frac{\left( CD+\frac{AB}{2} \right)BC}{2}=\frac{3}{12}C{C}'.CD.CB=\frac{3}{12}V\).

\({{S}_{BM{C}'}}=\frac{1}{2}BM.{C}'{B}'=\frac{1}{2}\frac{B{B}'}{2}.BC=\frac{B{B}'.BC}{4}\)\(\Rightarrow {{V}_{N.BM{C}'}}=\frac{1}{3}NB.{{S}_{BM{C}'}}=\frac{1}{3}\frac{BA}{2}.\frac{B{B}'.BC}{4}=\frac{V}{24}\).

\(\Rightarrow {{V}_{1}}={{V}_{{C}'.CBND}}+{{V}_{N.BM{C}'}}=\frac{3V}{12}+\frac{V}{24}=\frac{7V}{24}\) \(\Rightarrow {{V}_{2}}=V-\frac{7V}{24}=\frac{17V}{24}\) \(\Rightarrow \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{7V}{24}:\frac{17V}{24}=\frac{7}{17}\).

Chọn B.