Câu hỏi
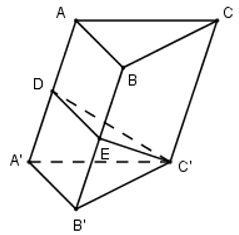
Xét khối lăng trụ tam giác \(ABC.A’B’C’\). Mặt phẳng đi qua \(C’\) và các trung điểm \(AA’, BB’\) chia khối lăng trụ thành hai phần có tỉ số thể tích bằng:
- A \(\dfrac{1}{2}\)
- B \(\dfrac{1}{3}\)
- C \(\dfrac{2}{3}\)
- D \(1\)
Phương pháp giải:
+) So sánh \({{V}_{C'.ABB'A'}}\) và \({{V}_{ABC.A'B'C'}}\)
+) So sánh \({{V}_{C'.A'B'ED}}\) và \({{V}_{C'.ABB'A'}}\)
+) Suy ra kết quả.
Lời giải chi tiết:
Gọi D và E lần lượt là trung điểm của AA’ và BB’, khi đó mặt phẳng (C’DE) chia khối lăng trụ tam giác ban đầu thành 2 khối: C’.A’B’ED và ABC.C’DE.
Ta có: \({{V}_{C'.ABC}}=\dfrac{1}{3}{{V}_{ABC.A'B'C'}}\Rightarrow {{V}_{C'.ABB'A'}}=\dfrac{2}{3}{{V}_{ABC.A'B'C'}}\)
Mà \({{V}_{C'.A'B'ED}}=\dfrac{1}{2}{{V}_{C'.ABB'A'}}\) (do \({{S}_{A'B'ED}}=\dfrac{1}{2}{{S}_{ABB'A'}}\))
\(\Rightarrow {{V}_{C'.A'B'ED}}=\dfrac{1}{3}{{V}_{ABC.A'B'C'}}\Rightarrow \dfrac{{{V}_{C'.A'B'ED}}}{{{V}_{ABC.C'DE}}}=\dfrac{1}{2}\)
Chọn A.