Câu hỏi
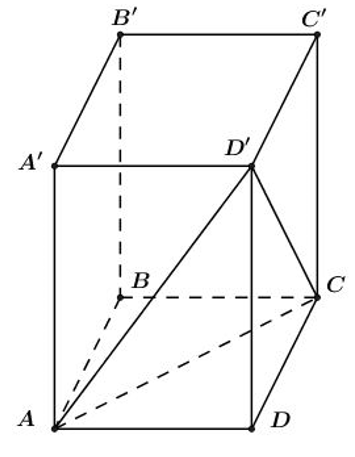
Cho hình lập phương ABCD.A’B’C’D’ có diện tích tam giác ACD’ bằng \({{a}^{2}}\sqrt{3}.\) Tính thể tích V của hình lập phương.
- A \(V=8{{a}^{3}}\)
- B \(V={{a}^{3}}\)
- C \(V=2\sqrt{2}{{a}^{3}}\)
- D \(V=4\sqrt{2}{{a}^{3}}\)
Phương pháp giải:
Thể tích của hình lập phương cạnh a: \(V={{a}^{3}}.\)
Lời giải chi tiết:
Gọi cạnh của hình lập phương là \(x\)
Khi đó \({{V}_{ABCD.A'B'C'D'}}={{x}^{3}}.\)
Xét tam giác AA’D vuông tại A ta có:
\(AD'=\sqrt{DD{{'}^{2}}+A{{D}^{2}}}=\sqrt{{{x}^{2}}+{{x}^{2}}}=x\sqrt{2}.\)
Tương tự có: \(D'C=AC=x\sqrt{2}.\)
\(\Rightarrow AD'C\) là tam giác đều cạnh \(x\sqrt{2}.\)
\(\begin{align} & \Rightarrow {{S}_{D'AC}}=\frac{{{\left( x\sqrt{2} \right)}^{2}}\sqrt{3}}{4}={{a}^{2}}\sqrt{3} \\ & \Leftrightarrow x=2{{a}^{2}}\Leftrightarrow x=a\sqrt{2}. \\ & \Rightarrow {{V}_{ABCD.A'B'C'D'}}={{x}^{3}}={{\left( a\sqrt{2} \right)}^{3}}=2\sqrt{2}{{a}^{3}}. \\ \end{align}\)
Chọn C.