Câu hỏi
Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng a. Gọi O và O’ lần lượt là tâm các hình vuông ABCD và A’B’C’D’. Gọi M và N lần lượt là trung điểm của các cạnh B’C’ và CD. Tính thể tích khối tứ diện OO’MN.
- A \(\dfrac{{{a^3}}}{{24}}.\)
- B \(\dfrac{{{a^3}}}{8}.\)
- C \({a^3}.\)
- D \(\dfrac{{{a^3}}}{{12}}.\)
Phương pháp giải:
- Tính tỉ số diện tích thông qua các dữ kiện về chiều cao, diện tích đáy.
Lời giải chi tiết:
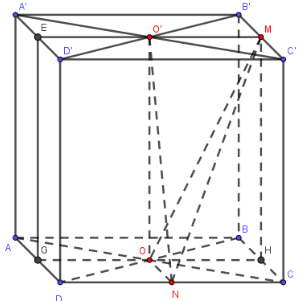
Gọi E, G, H lần lượt là trung điểm của A’D’, AD, BC.
Khi đó, \(\dfrac{{{V_{N.O'OM}}}}{{{V_{N.EMHG}}}} = \dfrac{1}{4}\) ( do \(\dfrac{{{S_{O'OM}}}}{{{S_{EMHG}}}} = \dfrac{1}{4}\)).
Mà \(\dfrac{{{V_{N.EMHG}}}}{{{V_{N.ABB'A'}}}} = \dfrac{1}{2}\) (do \({d_{(N,(EMHG))}} = \dfrac{1}{2}{d_{(N,(ABB'A'))}}\) và hình vuông EMHG bằng hình vuông ABB’A’)
Suy ra, \({V_{N.O'OM}} = \dfrac{1}{4}.\dfrac{1}{2}.{V_{N.ABB'A'}} = \dfrac{1}{4}.\dfrac{1}{2}.\dfrac{1}{3}.{V_{ABCD.A'B'C'D'}} = \dfrac{1}{{24}}{a^3}\)
Chọn: A.
Câu hỏi trước
