Câu hỏi
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD.
- A \(V = \dfrac{1}{3}.\)
- B \(V = \dfrac{2}{3}.\)
- C \(V = \dfrac{4}{3}.\)
- D \(V = \dfrac{1}{6}.\)
Phương pháp giải:
- Lập tỉ số thể tích của 2 khối chóp.
Lời giải chi tiết:
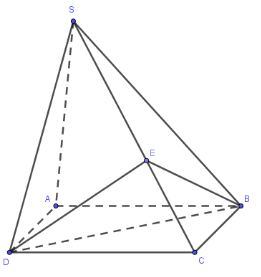
\(\left\{ \begin{array}{l}
\dfrac{{{V_{S.BDE}}}}{{{V_{S.BCD}}}} = \dfrac{{SE}}{{SC}} = \dfrac{2}{3}\\
\dfrac{{{V_{S.BCD}}}}{{{V_{S.ABCD}}}} = \dfrac{{\dfrac{1}{3}h.{S_{BCD}}}}{{\dfrac{1}{3}h.{S_{ABCD}}}} = \dfrac{{{S_{BCD}}}}{{{S_{ABCD}}}} = \dfrac{1}{2}
\end{array} \right. \Rightarrow {V_{S.BDE}} = \dfrac{2}{3}.\dfrac{1}{2}{V_{S.ABCD}} = \dfrac{1}{3}\)
Chọn: A.
Câu hỏi trước
