Câu hỏi
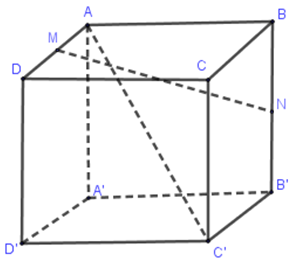
Cho hình lập phương \(ABCD.A'B'C'D'\). Gọi \(M,N\) lần lượt là trung điểm \(AD,BB'\). Côsin của góc hợp bởi \(MN\) và \(AC'\) là:
- A \(\frac{\sqrt{3}}{3}\)
- B \(\frac{\sqrt{2}}{3}\)
- C \(\frac{\sqrt{5}}{3}\)
- D \(\frac{\sqrt{2}}{4}\)
Phương pháp giải:
Sử dụng công thức \(\cos \left( \overrightarrow{a};\overrightarrow{b} \right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|}\).
Lời giải chi tiết:
Ta có: \(\cos \left( \overrightarrow{MN},\overrightarrow{AC'} \right)=\frac{\overrightarrow{MN}.\overrightarrow{AC'}}{\left| \overrightarrow{MN} \right|.\left| \overrightarrow{AC'} \right|}\)
Gọi cạnh của hình lập phương bằng a.
\(AM\bot \left( ABB'A' \right)\Rightarrow AM\bot AN\Rightarrow \Delta AMN\) vuông tại A
\(\begin{align} & M{{N}^{2}}=M{{A}^{2}}+A{{N}^{2}}=M{{A}^{2}}+A{{B}^{2}}+B{{N}^{2}} \\ & =\frac{{{a}^{2}}}{4}+{{a}^{2}}+\frac{{{a}^{2}}}{4}=\frac{3{{a}^{2}}}{2}\Rightarrow MN=\frac{a\sqrt{3}}{\sqrt{2}} \\ \end{align}\)
\(B'C'\bot \left( ABB'A' \right)\Rightarrow B'C'\bot AB'\Rightarrow \Delta B'C'\) vuông tại B’.
\(\begin{align} & C'{{A}^{2}}=C'B{{'}^{2}}+B'{{A}^{2}}=C'B{{'}^{2}}+B'{{B}^{2}}+B{{A}^{2}} \\ & ={{a}^{2}}+{{a}^{2}}+{{a}^{2}}=3{{a}^{2}}\Rightarrow C'A=a\sqrt{3} \\ \end{align}\)
Lại có:
\(\begin{align} & \overrightarrow{MN}.\overrightarrow{AC'}=\left( \overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN} \right)\left( \overrightarrow{AB}+\overrightarrow{BB'}+\overrightarrow{B'C'} \right) \\ & =\overrightarrow{MA}.\overrightarrow{AB}+A{{B}^{2}}+\overrightarrow{BN}.\overrightarrow{AB}+\overrightarrow{MA}.\overrightarrow{BB'}+\overrightarrow{AB}.\overrightarrow{BB'}+\overrightarrow{BN}.\overrightarrow{BB'}+\overrightarrow{MA}.\overrightarrow{B'C'}+\overrightarrow{AB}.\overrightarrow{B'C'}+\overrightarrow{BN}.\overrightarrow{B'C'} \\ \end{align}\)
Mà \(\overrightarrow{MA}.\overrightarrow{AB}=\overrightarrow{BN}.\overrightarrow{AB}=\overrightarrow{MA}.\overrightarrow{BB'}=\overrightarrow{AB}.\overrightarrow{BB'}=\overrightarrow{AB}.\overrightarrow{B'C'}=\overrightarrow{BN}.\overrightarrow{B'C'}=0\) (do các tích vô hướng của các vector vuông góc)
Nên \(\overrightarrow{MN}.\overrightarrow{AC'}=A{{B}^{2}}+\overrightarrow{BN}.\overrightarrow{BB'}+\overrightarrow{MA}.\overrightarrow{B'C'}={{a}^{2}}+\frac{{{a}^{2}}}{2}-\frac{{{a}^{2}}}{2}={{a}^{2}}\)
Vậy \(\cos \left( \overrightarrow{MN},\overrightarrow{AC'} \right)=\frac{\overrightarrow{MN}.\overrightarrow{AC'}}{\left| \overrightarrow{MN} \right|.\left| \overrightarrow{AC'} \right|}=\frac{{{a}^{2}}}{\frac{a\sqrt{3}}{\sqrt{2}}.a\sqrt{3}}=\frac{\sqrt{2}}{3}\)
Chọn B.