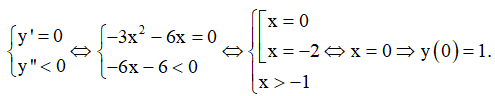Câu hỏi
Cho hàm số \(y=-{{x}^{3}}-3{{x}^{2}}+1\) có điểm cực đại là:
- A \(x=0\)
- B \(\left( 0;\,\,1 \right)\)
- C \(x=-2\)
- D \(\left( -2;-19 \right)\)
Phương pháp giải:
Hoành độ các điểm cực trị của hàm số là nghiệm của phương trình \(y'=0.\)
Tung độ của điểm cực trị có hoành độ \(x={{x}_{0}}\) là \({{y}_{0}}=y\left( {{x}_{0}} \right).\)
Ta có: \(x={{x}_{0}}\) là điểm cực đại của hàm số \(\Leftrightarrow \left\{ \begin{align} & y'\left( {{x}_{0}} \right)=0 \\ & y''\left( {{x}_{0}} \right)
Lời giải chi tiết:
Ta có:
Vậy điểm cực đại của hàm số là \({x_{CD}} = 0\).
Chọn A.
Câu hỏi trước
