Phương pháp giải:

+) Sử dụng công thức \(\dfrac{1}{{n\left( {n + 1} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}\)  thu gọn biểu thức cần tính giới hạn.

+) Sử dụng MTCT để tính giới hạn

Lời giải chi tiết:

Ta có

\(\begin{array}{l}
\dfrac{1}{{1.2}} = 1 - \dfrac{1}{2}\\
\dfrac{1}{{2.3}} = \dfrac{1}{2} - \dfrac{1}{3}\\
\dfrac{1}{{3.4}} = \dfrac{1}{3} - \dfrac{1}{4}\\
....\\
\dfrac{1}{{n\left( {n + 1} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}\\
\Rightarrow \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{n\left( {n + 1} \right)}} = 1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + ... + \dfrac{1}{n} - \dfrac{1}{{n + 1}} = 1 - \dfrac{1}{{n + 1}}\\
\Rightarrow \lim \left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{n\left( {n + 1} \right)}}} \right) = \lim \left( {1 - \dfrac{1}{{n + 1}}} \right)
\end{array}\).

Nhập \(1 - \dfrac{1}{{n + 1}}\) vào MTCT , nhấn phím [CALC], chọn \(x = {10^{10}}\)  ta được kết quả 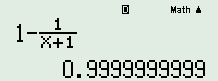 \( \Rightarrow \lim \left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{n\left( {n + 1} \right)}}} \right) = 1\)

Chọn A.