Phương pháp giải:

Sử dụng MTCT

Lời giải chi tiết:

Nhấn tổ hợp phím [SHIFT] [MODE] [4] chuyển máy tính sang chế độ Rad.

Sử dụng MTC, nhập \(\dfrac{{\sin n}}{n}\) 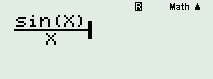  :, nhấn phím [CALC], chọn x = 1000  ta được  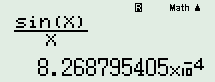\( \Rightarrow \lim \dfrac{{\sin n}}{n} = 0\).

Thử từng đáp án ta có:

Đáp án A: 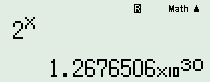\( \Rightarrow \lim {2^n} =  + \infty \)

Đáp án B: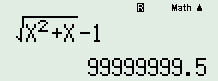 \( \Rightarrow \lim \left( {\sqrt {{n^2} + n}  - 1} \right) =  + \infty \)

Đáp án C: 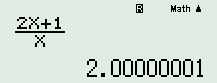 \( \Rightarrow \lim \dfrac{{2n + 1}}{n} = 2\)

Đáp án D: \( \Rightarrow \lim {\left( {\dfrac{1}{2}} \right)^n} = 0 = \lim \dfrac{{\sin n}}{n} = 0\)

Chọn D.