Phương pháp giải:

+) Rút gọn tử số bằng cách áp dụng công thức tổng n số hạng đầu tiên của cấp số nhân ${S_n} = \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}$

+) Sử dụng MTCT để tìm giới hạn.

Lời giải chi tiết:

Ta có $1 + 2 + {2^2} + {2^3} + ... + {2^n} = \dfrac{{1\left( {1 - {2^n}} \right)}}{{1 - 2}} = {2^n} - 1$

$\Rightarrow \lim \dfrac{{1 + 2 + {2^2} + {2^3} + ... + {2^n}}}{{{5^{2n + 3}} + 1}} = \lim \dfrac{{{2^n} - 1}}{{{5^{2n + 3}} + 1}}$

 Sử dụng MTC, nhập $\dfrac{{{2^n} - 1}}{{{5^{2n + 3}} + 1}}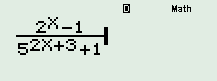$  : , nhấn phím [CALC], chọn x = 10 ta được  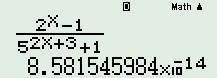$\Rightarrow \lim \dfrac{{{2^n} - 1}}{{{5^{2n + 3}} + 1}} = 0$.

Chọn D.