Phương pháp giải:

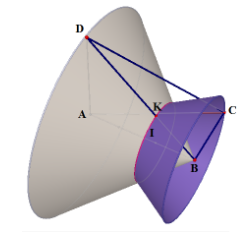
Do \(AD \bot (ABC) \Rightarrow AD \bot AB \Rightarrow \) Khi quay tam giác ABD quanh AB sẽ tạo ra hình nón có đỉnh là B và đáy có bán kính là AD.

Do tam giác ABC vuông tại B \( \Rightarrow BC \bot AB \Rightarrow \) Khi quay tam giác ABC quanh AB sẽ tạo ra hình nón có đỉnh là A và đáy có bán kính là BC.

Phần chung của 2 khối nón này chính là 2 khối nón: đỉnh lần lượt là B và A, bán kính đáy đều là IK (như hình vẽ)

Lời giải chi tiết:

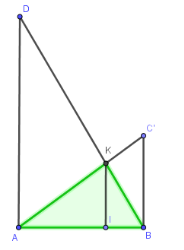
* Xét  mặt phẳng (ABD):

Gọi C’ là điểm ở trong (ABD) sao cho: C’B vuông góc AB và C’B = BC = a.

Gọi \(K = AC' \cap BD,\,\,IK \bot AB\,\,(I \in AB)\)

Theo Ta – lét ta có:  \(\dfrac{{IK}}{{BC'}} = \dfrac{{IA}}{{AB}} = 1 - \dfrac{{IB}}{{AB}} = 1 - \dfrac{{KI}}{{3BC'}} \Leftrightarrow \dfrac{4}{3}\dfrac{{KI}}{{BC'}} = 1 \Leftrightarrow \dfrac{{KI}}{{BC'}} = \dfrac{3}{4} \Rightarrow IK = \dfrac{3}{4}a\)

Thể tích của phần chung là:

\(V = \dfrac{1}{3}\pi I{K^2}.IA + \dfrac{1}{3}\pi I{K^2}.IB = \dfrac{1}{3}\pi I{K^2}.AB = \dfrac{1}{3}\pi .{\left( {\dfrac{{3a}}{4}} \right)^2}.a\sqrt 3  = \dfrac{{3\sqrt 3 \pi {a^3}}}{{16}}\)

Chọn: B.