Câu hỏi
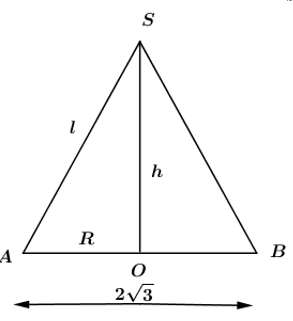
Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền bằng \(2\sqrt{3}.\) Thể tích của khối nón này là:
- A \(\pi \sqrt{3}\)
- B \(9\pi \sqrt{3}\)
- C \(6\pi \sqrt{3}\)
- D \(3\pi \sqrt{3}\)
Phương pháp giải:
+) Thiết diện qua trục của hình nón luôn là tam giác cân tại đỉnh của hình nón.
+) Theo đề bài ta có thiết diện là tam giác vuông cân \(\Rightarrow \) đường kính đáy = cạnh huyền của thiết diện.
+) Công thức tính thể tích của hình nón: \(V=\frac{1}{3}\pi {{R}^{2}}h.\)
+) Áp dụng định lý Pi-ta-go để tính chiều cao của hình nón: \(h=\sqrt{{{l}^{2}}-{{R}^{2}}}.\)
Lời giải chi tiết:
Ta có: \(2R=2\sqrt{3}\Rightarrow R=\sqrt{3}.\)
Áp dụng định lý Pi-ta-go cho tam giác SAB vuông cân tại S có:
\(2{{l}^{2}}={{\left( 2R \right)}^{2}}\Leftrightarrow l=R\sqrt{2}=\sqrt{6}.\)
Áp dụng đính lý Pi-ta-go cho tam giác SAO vuông tại O ta có:
\(\begin{align} & h=\sqrt{{{l}^{2}}-{{R}^{2}}}=\sqrt{6-3}=\sqrt{3}. \\ & \Rightarrow V=\frac{1}{3}.\pi {{R}^{2}}h=\frac{1}{3}\pi .{{\left( \sqrt{3} \right)}^{2}}.\sqrt{3}=\pi \sqrt{3}. \\ \end{align}\)
Chọn A.