Câu hỏi
Cho phương trìn \({x^3} - 3{x^2} + 1 - m = 0\,\,(1).\). Điều kiện của tham số m để phương trình (1) có 3 nghiệm phân biệt thỏa mãn \({x_1} < 1 < {x_2} < {x_3}\) là:
- A \( - 3 \le m \le - 1.\)
- B \( - 3 < m < - 1.\)
- C \(m = - 1.\)
- D \( - 1 < m < 3.\)
Phương pháp giải:
- Sử dụng đồ thị hàm số để giải.
Lời giải chi tiết:
Ta có:
\({x^3} - 3{x^2} + 1 - m = 0\,\,\,(1) \Leftrightarrow {x^3} - 3{x^2} + 1 = m\)
Số nghiệm của phương trình (1) bằng số giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) với đường thẳng \(y = m\)
Quan sát đồ thị bên dưới , ta thấy:
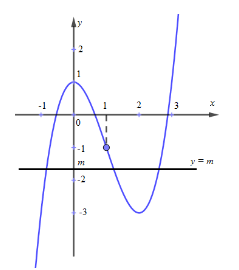
Để đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) cắt đường thẳng \(y = m\) tại 3 điểm có hoành độ thỏa mãn \({x_1} < 1 < {x_2} < {x_3}\) thì \( - 3 < m < - 1.\)
Chọn: B.
Câu hỏi trước
