Câu hỏi
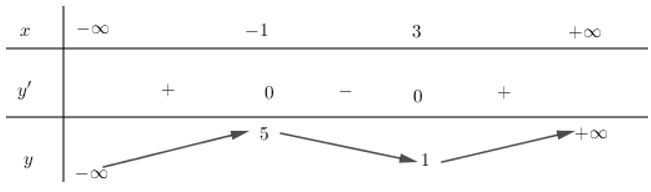
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
Tìm m để phương trình \(\left| f\left( x \right) \right|=m\) có 3 nghiệm phân biệt?
- A \(\left[ \begin{align} & m\ge 5 \\ & m=1 \\ \end{align} \right.\)
- B \(\left[ \begin{align} & m\ge 5 \\ & m\le 1 \\ \end{align} \right.\)
- C
\(1<m<5\)
- D \(\left[ \begin{align} & m=1 \\ & m=5 \\ \end{align} \right.\)
Phương pháp giải:
Từ bảng biến thiên ta suy luận được đồ thị hàm số \(y=f\left( x \right)\) sau đó vẽ đồ thị hàm số \(y=\left| f\left( x \right) \right|\) bằng cách như sau:
Bước 1: Vẽ đồ thị (C) của hàm số y = f(x)
Bước 2: Giữ nguyên đồ thị (C) phía trên trục hoành.
Bước 3: Lấy đối xứng với phần đồ thị (C) phía dưới trục hoành qua trục hoành (bỏ đi phần đồ thị phía dưới trục hoành)
Bước 4: Hợp 2 phần đồ thị trên chính là đồ thị hàm số \(y=\left| f\left( x \right) \right|\)
Lời giải chi tiết:
+) Đây là đồ thị hàm số bậc 3: \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\)
+) Đồ thị hàm số đi qua điểm (-1;5) nên \(-a+b-c+d=5\)
+) Đồ thị hàm số đi qua điểm (3;1) nên ta có: \(27a+9b+3c+d=1\,\)
\(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\Rightarrow y'=3a{{x}^{2}}+2bx+c\)
Vì (-1;5) là điểm cực đại của đồ thị hàm số nên \(x=-1\) là nghiệm của \(y'\Rightarrow y'\left( -1 \right)=0\Leftrightarrow 3a-2b+c=0\).
+) Đồ thị hàm số có điểm cực tiểu là (3;1) nên \(x=3\) là nghiệm của \(y'\) ta có: \(y'\left( 3 \right)=0\Leftrightarrow 27a+6b+c=0\)
Ta có hệ
\(\left\{ \begin{array}{l} - a + b - c + d = 5\\27a + 9b + 3c + d = 1\\3a - 2b + c = 0\\27a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{8}\\b = - \frac{3}{8}\\c = - \frac{9}{8}\\d = \frac{{35}}{8}\end{array} \right.\)
Từ đó ta có hàm số cần tìm là: \(y=\frac{1}{8}{{x}^{3}}-\frac{3}{8}{{x}^{2}}-\frac{9}{8}x+\frac{35}{8}\)
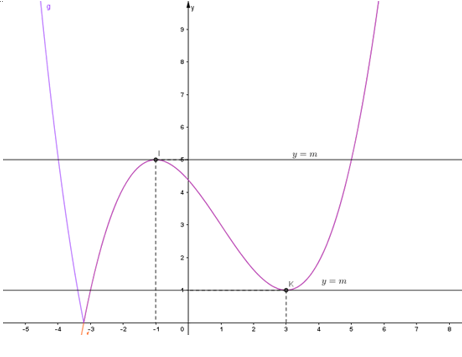
Vẽ đồ thị hàm số: \(y=\left| \frac{1}{8}{{x}^{3}}-\frac{3}{8}{{x}^{2}}-\frac{9}{8}x+\frac{35}{8} \right|\) ta được:
Vậy dựa vào đồ thị hàm số vừa vẽ: để phương trình \(\left| f\left( x \right) \right|=m\) có 3 nghiệm phân biệt thì 2 đồ thị \(y=\left| f\left( x \right) \right|\) và đồ thi \(y=m\) cắt nhau tại 3 điểm phân biệt.
Từ đó ta tìm được m = 1 hoặc m = 5
Vậy với m = 1 hoặc m = 5 thì phương trình có 3 nghiệm phân biệt.
Chọn D.