Câu hỏi
Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 340 và 380. (Hình minh họa như hình bên)
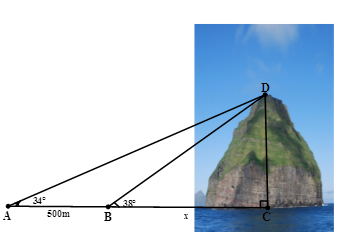
- A Chiều cao của ngọn núi là 2667,7 mét.
- B Chiều cao của ngọn núi là 2647,7 mét.
- C Chiều cao của ngọn núi là 2467,7 mét.
- D Chiều cao của ngọn núi là 2447,7 mét.
Lời giải chi tiết:

Đặt: BC = x (m)
\(AC = AB + BC = 500 + {x^{}}\left( m \right)\)
Xét tam giác vuông ACD, ta có:
\(\tan CAD = \dfrac{{CD}}{{AC}} \Rightarrow CD = AC.\tan CAD \Leftrightarrow CD = \left( {500 + x} \right).tan{34^0}\) (1)
Xét tam giác vuông BCD, ta có:
\(\tan CBD = \dfrac{{CD}}{{BC}} \Rightarrow CD = BC.\tan CBD \Leftrightarrow CD = x.tan{38^0}\) (2)
Từ (1) và (2)
\(\begin{array}{l}
\Rightarrow \left( {500 + x} \right).tan{34^0} = x.t{\rm{an3}}{8^0}\\
\Leftrightarrow 500.\tan {34^0} + x.tan{34^0} = x.\tan {38^0}\\
\Leftrightarrow x.\tan {38^0} - x.tan{34^0} = 500.\tan {34^0}\\
\Leftrightarrow x.\left( {tan{{38}^0} - tan{{34}^0}} \right) = 500.\tan {34^0}\\
\Leftrightarrow x = \dfrac{{500.\tan {{34}^0}}}{{tan{{38}^0} - tan{{34}^0}}} = 3158,5m
\end{array}\)
Chiều cao của ngọn núi là: \(CD = 3158,5.\tan {38^0} = 2467,{7^{}}\left( m \right)\)
Vậy: Chiều cao của ngọn núi là 2467,7 mét.







