Câu hỏi
Vào khoảng năm 200 trước Công nguyên, Ơ-ra-tô-xten, một nhà toán học và thiên văn học Hi lạp đã ước lượng được "chu vi" của Trái Đất (chu vi đường xích đạo) nhờ hai quan sát sau:
a) Một ngày trong năm, ông để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (nay gọi là Át-xu-an), tức là tia sáng chiếu thẳng đứng
b) Cùng lúc đó ở thành phố A-lếch-xăng-đri-a cách Xy-en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m
Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của Trái Đất (Trên hình), điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trưng cho thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB

- A 407,41km
- B 407410km
- C 40,741km
- D 40741km
Lời giải chi tiết:
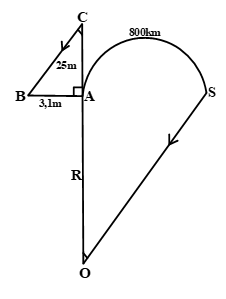
Do cung AB quá nhỏ (3,1m) nên ta có thể xem như là một đoạn thẳng.
trong tam giác vuông ABC, ta có:
\(\tan \widehat {ACB} = \dfrac{{AB}}{{AC}} = \dfrac{{3,1}}{{25}} = 0,124 \Rightarrow \widehat {ACB} \approx 7,{069^0}\)
Do các tia sáng đến từ mặt trời coi như song song nên ta có:CB // SO
Suy ra: \(\widehat {ACB} = \widehat {AOS} \approx 7,{069^0}\) (hai góc so le trong)
Ta có:Độ dài cung AS = 800km ứng với góc 7,0690 ở tâm
Chu vi Trái Đất P ứng với góc 3600
Suy ra, chu vi của Trái Đất là:
\(P = \dfrac{{360.800}}{{7,069}} \approx {40741^{}}\left( {km} \right)\)







