Câu hỏi
1. Một khối u của một căn bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) 8,3cm (hình vẽ)

1a) Hỏi góc tạo bởi chùm tia với mặt da?
1b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?
2. Trước nhà thầy Tưởng có một cây cột điện cao 9m bị cơn bão Tembin vừa qua làm gãy ngang thân, ngọn cây cột điện chạm đất cách gốc 3m. Hỏi điểm gãy ngang của cây cột điện cách gốc bao nhiêu?

- A 1a) 34,50
1b)10,1cm
2) 5 mét
- B 1a) 34,50
1b)12,1cm
2) 4 mét
- C 1a) 34,50
1b) 10,1cm
2) 4 mét
- D 1a) 35,50
1b) 10,1cm
2) 6 mét
Lời giải chi tiết:
1.1a)
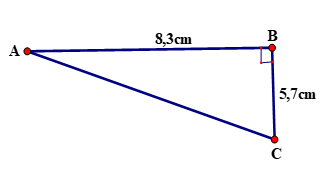
Đặt tên vị trí các điểm A, B, C như trong hình vẽ, trong đó:
AB = 8,3cm, BC = 5,7cm .
Đường đi của chùm tia tới khối u tương ứng với độ dài của đoạn AC trên hình, góc tạo bởi chùm tia với mặt da là góc BAC.
Xét tam giác vuông ABC, ta có:
\(\tan BAC=\frac{BC}{AB}=\frac{5,7}{8,3}\Rightarrow \angle BAC\approx 34,{{5}^{0}}\)
Vậy góc tạo bởi chùm tia với mặt da gần bằng 34,50
1.1b)
· Áp dụng định lý Pitago cho tam giác vuông ABC, ta có:
\(AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{8,{{3}^{2}}+5,{{7}^{2}}}=\sqrt{101,38}\approx 10,1cm\)
Vậy Chùm tia phải đi một đoạn dài gần bằng 10,1cm để đến được khối u.
2. Vẽ lại hình minh họa và đặt tên các vị trí tương ứng như trong hình vẽ. Trong đó, AC’ = m là chiều cao cây cột điện, AC = 3m là khoảng từ ngọn cây cột điện chạm đất đến gốc cây, BC là cây cột điện bị gãy

AB là khoảng cách từ điểm gãy của cây cột điện đến gốc cây. Đặt AB = x (m), x > 0.
\(\Rightarrow BC'=BC=9-x\) (m)
Áp dụng định lý Pitago vào trong tam giác vuông ABC, ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {x^2} + {3^2} = {\left( {9 - x} \right)^2}\\ \Leftrightarrow {x^2} + 9 = 81 - 18x + {x^2}\\ \Leftrightarrow 18x = 72\\ \Leftrightarrow x = {4^{}}\left( {t/m} \right)\end{array}\)
Vậy điểm gãy ngang của cây cột điện cách gốc bằng 4 mét.







