Câu hỏi
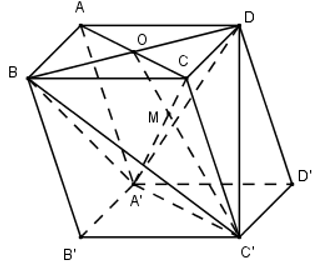
Cho hình hộp ABCD.A’B’C’D’. Tỉ số thể tích giữa tứ diện CC’BD và tứ diện BDA’C’ bằng bao nhiêu ?
- A \(\frac{1}{2}\)
- B \(\frac{1}{3}\)
- C \(1\)
- D \(\frac{1}{4}\)
Phương pháp giải:
\(A;B\notin \left( P \right),AB\cap \left( P \right)=M\Rightarrow \frac{d\left( A;\left( P \right) \right)}{d\left( B;\left( P \right) \right)}=\frac{MA}{MB}\)
Lời giải chi tiết:
Gọi \(O=AC\cap BD\Rightarrow C'O\subset \left( BC'D \right)\)
Trong mp(ACC’A’) gọi \(M=A'C\cap C'O\),
mà \(C'O\subset \left( BC'D \right)\Rightarrow M=A'C\cap \left( BC'D \right)\) .
Ta có \(\frac{{{V}_{CC'BD}}}{{{V}_{BDA'C'}}}=\frac{{{V}_{C.BC'D}}}{{{V}_{A'.BC'D}}}=\frac{\frac{1}{3}d\left( C;\left( BC'D \right) \right).{{S}_{BC'D}}}{\frac{1}{3}d\left( A';\left( BC'D \right) \right).{{S}_{BC'D}}}=\frac{d\left( C;\left( BC'D \right) \right)}{d\left( A';\left( BC'D \right) \right)}=\frac{MC}{MA'}\)
Theo định lí Ta-let (OC // A’C’) ta có \(\frac{MC}{MA'}=\frac{OC}{A'C'}=\frac{1}{2}\Rightarrow \frac{{{V}_{CC'BD}}}{{{V}_{BDA'C'}}}=\frac{1}{2}\)
Chọn A.