Câu hỏi
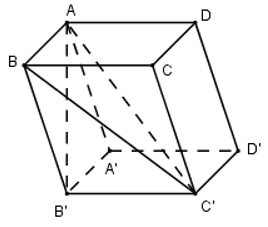
Cho thể tích khối hộp ABCD.A’B’C’D’ là V. Tính thể tích khối tứ diện ABB’C’ theo V.
- A \(\frac{V}{6}\)
- B \(\frac{V}{3}\)
- C \(\frac{V}{27}\)
- D \(\frac{V}{9}\)
Phương pháp giải:
Sử dụng công thức thể tích khối chóp \(V=\frac{1}{3}Bh\) trong đó B là diện tích đáy và h là chiều cao của khối chóp và công thức tình thể tích hình hộp \(V=Bh\) trong đó B là diện tích đáy và h là chiều cao ứng với đáy đó.
Lời giải chi tiết:
\({{V}_{ABB'C'}}={{V}_{C'.ABB'}}=\frac{1}{3}d\left( C';\left( ABB' \right) \right).{{S}_{ABB'}}=\frac{1}{3}d\left( C';\left( ABB' \right) \right).\frac{1}{2}{{S}_{ABB'A'}}=\frac{1}{6}V\)
Chọn A.